AQA GCSE Balancing Moments(Physics)
Balancing Moments
A moment is the turning effect of a force.
Moments can be anticlockwise, or clockwise.
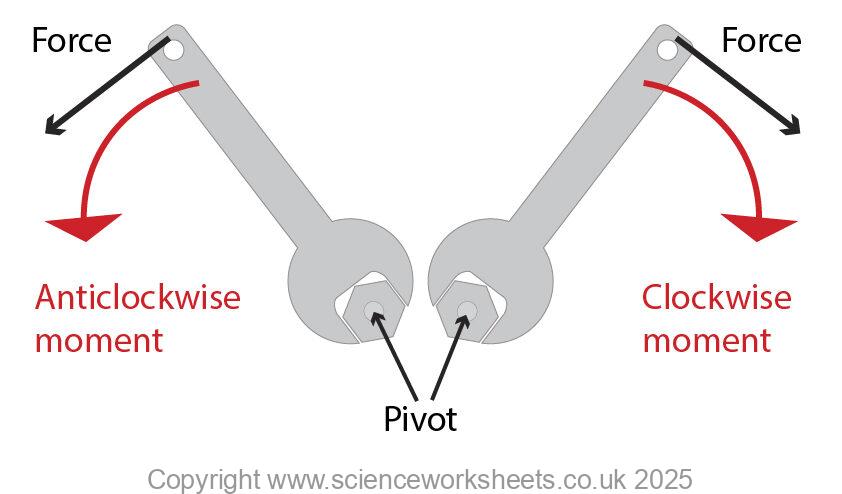
Principle of Moments.
when an object is balanced, the total clockwise moment about a point is equal to the total anticlockwise moment
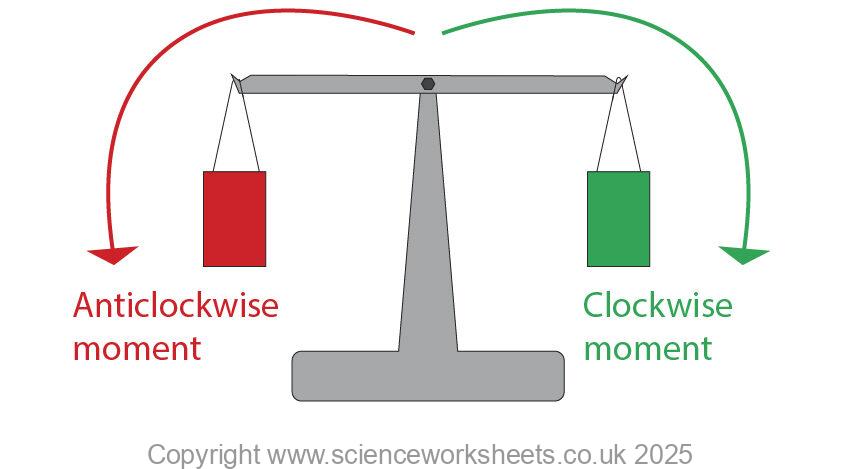
The object in this case in a static equilibrium because the anticlockwise moment is the same size as the clockwise moment the object does not turn.
Calculations using Principle of Moments
Moment, M = Force, F x distance,d
Anticlockwise moment = Clockwise moment
Force 1, F1 x distance 1, d1 = Force 2, F2 x distance 2, d2
Lets draw these distances and forces onto a diagram!
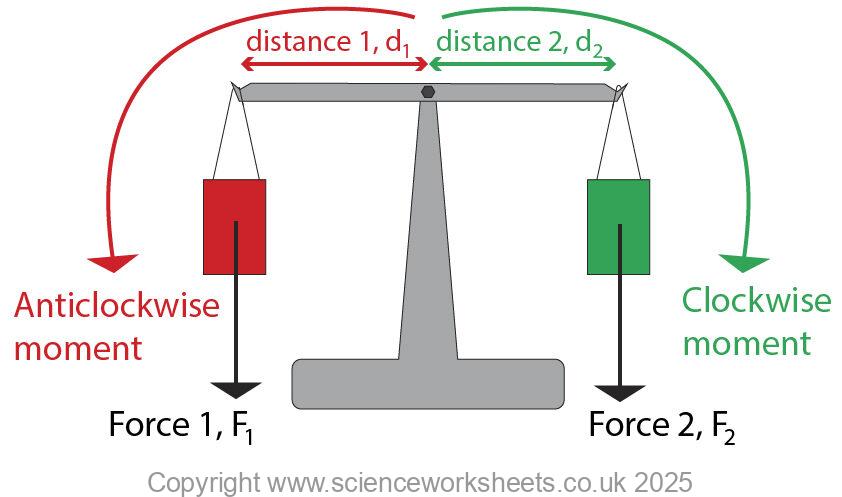
Example calculation
Use the diagram below to answer the following question
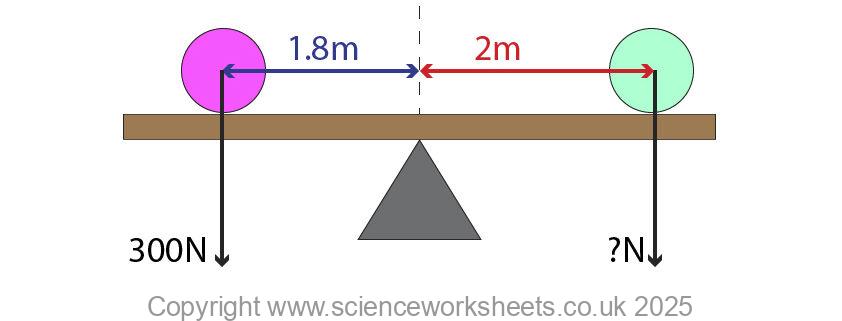
Calculate the weight of the light green ball on the right hand side
F1 = 300N, d1 = 1.8m, F2 = ? and d2 = 2m
F1 x d1 = F2 x d2
F2 = (F1 x d1)/d2
F2 = (300N x 1.8m)/2m = 270N
F2 = 270N
Example question 2
Use the image below to answer the following question
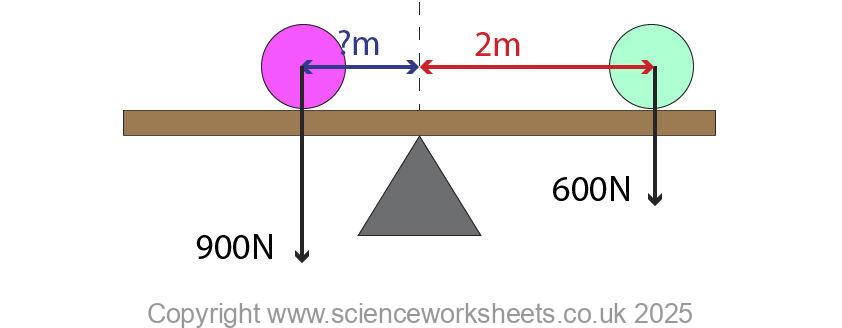
Calculate the distance between the pivot and the centre of the pink ball
F1 = 900N, d1 = ?m, F2 = 600N and d2 = 2m
F1 x d1 = F2 x d2
d1 = (F2 x d2)/F1
d1 = (600N x 2m)/900N = 1.33m
d1 = 1.33m
Practice questions
1.State the principle of moments
2. Use the image below to answer the following questions.
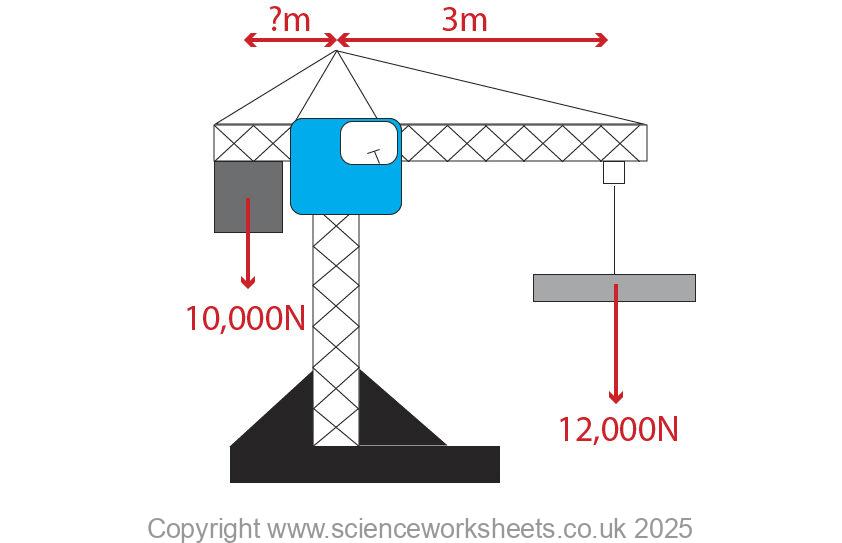
Calculate the length of the distance between the counterweight on the left hand side and the pivot. This unknown distance has been marked on the diagram as ?m.
3. Use the image below to help you to answer the following question
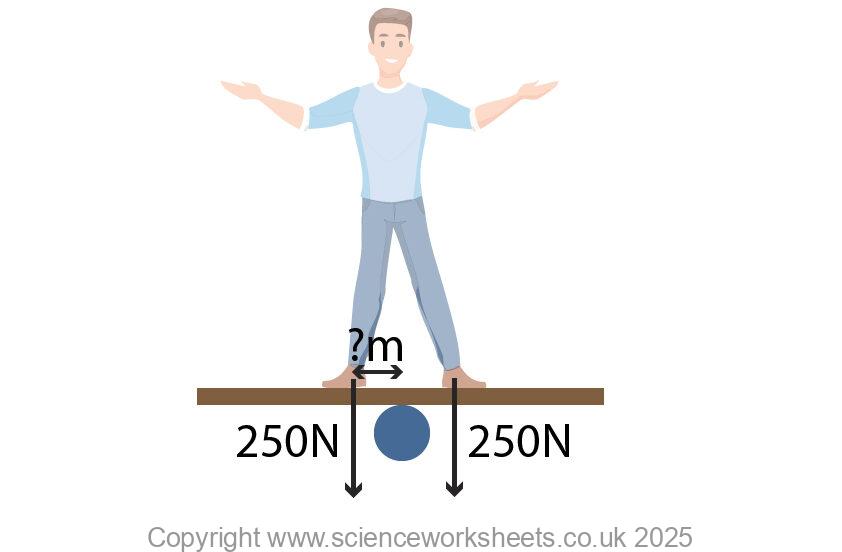
The man has a clockwise moment of 190Nm. Both of his feet are equal distance from the pivot. Calculate the distance between the pivot and his left foot. This distance has been labelled as ?m in the diagram above.
Absorption and Emission of EM Radiation
JJ Thomson and Plum pudding model
Ernest Rutherford and the Nuclear Model
Niels Bohr changing the Nuclear Model
Discovering the Proton and Neutron
Measuring radiation from radioactivity
Radiation types and properties
Random nature of radioactive decay
Radioactive contamination or irradiation
Hazards of contamination and irradiation
Studies on the effects of radiation on humans
Different half lives of radioactive isotopes
Nuclear Fission Chain Reaction
Writing nuclear fission equations
Drawing ray diagrams for a concave lens
Drawing Ray Diagram to produce a virtual image for a convex lens
Drawing ray diagram to produce a real image for a convex lens.
Specular and Diffuse Reflection
Seeing Coloured Objects Part 2
Viewing objects through coloured filters
Transparent, Translucent and Opaque