AQA GCSE Half Life Calculations

Half Life Calculations

This formula can be used for some of the count rate calculations

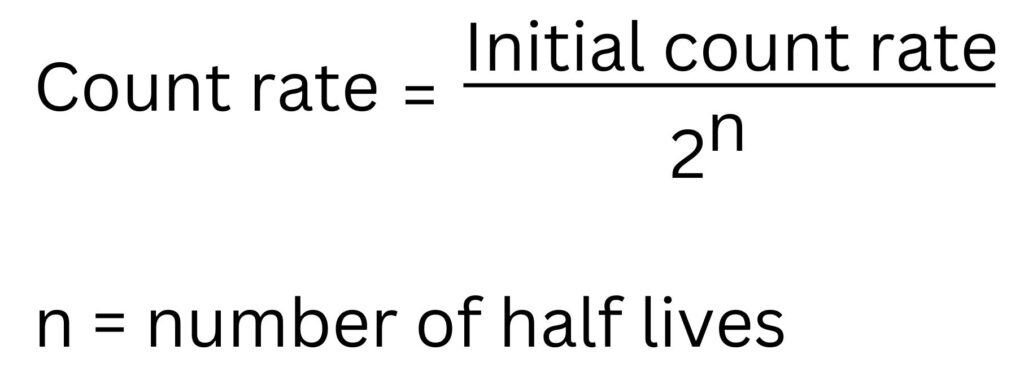
Sample question

A radioactive isotope has an initial count rate of 60000Bq, with a half life of 4 minutes. Calculate the count rate after 12 minutes

12 minutes/4 minutes = 3 half lives

Count rate = 60000/(2³)

Count rate = 7500

Net decline

In physics:

Net decline is the ratio of the number of isotopes present in a sample now to the initial number of isotopes present.

Sample Question

A sample of a radioactive isotope has 4 x 10¹⁸ atoms present. After two half lives there are 1 x 10¹⁸ atoms present. Calculate the net decline

It can also be defined in terms of count rate:

Net decline is the ratio of the count rate in a sample now to the initial count rate.

Sample Question

The initial count rate of a radioactive isotope is 120,000Bq. Calculate the net decline after 3 half lives

The count rate will halve after each half life. So, after 3 half lives we need to halve the 120,000Bq three times

120,000/2 = 60,000Bq

60,000Bq/2 = 30,000Bq

30,000Bq/2 = 15,000Bq

So, after 3 half lives, the count rate is 15,000Bq

Practice Questions

1. Polonium-210 has a half life of 140 days. If an original sample of Polonium-210 has an activity of 500Bq what will its activity be after 560 days.

2. A radioactive isotope undergoes a series of half lives. At the start there are 8 x 10³⁶ atoms of the isotope present. At a point later in time there are 1 x 10³⁶ atoms remaining. Calculate the net decline.

3. If the initial count rate is 200,000Bq. Calculate the net decline after 4 half lives