Answers to AQA GCSE Finding the resultant force, using the parallelogram rule Part 2 (Physics)
Finding the resultant force, using the parallelogram rule Part 2
We can use the parallelogram rule to find the resultant force of two forces that do not act along the same line.
Lets look at an example:
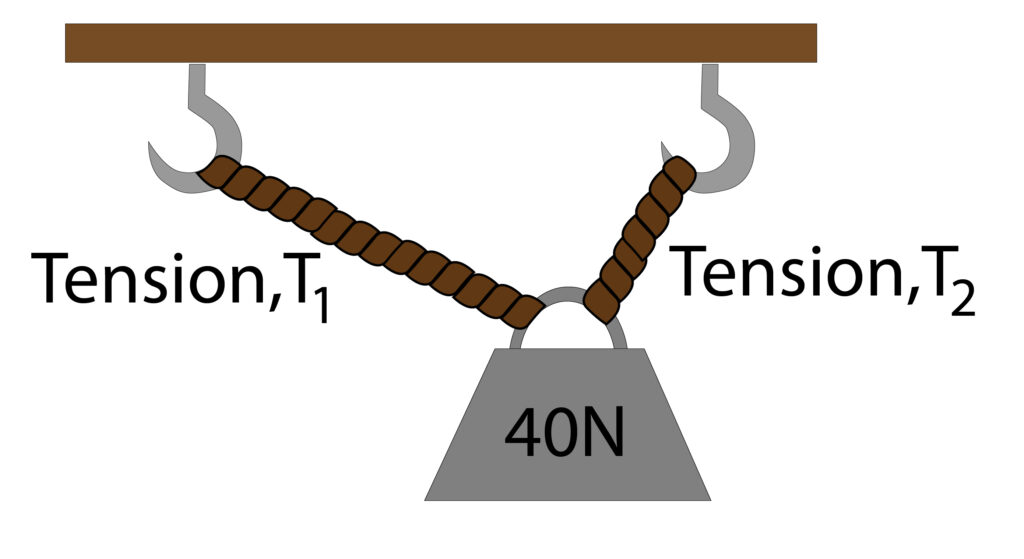
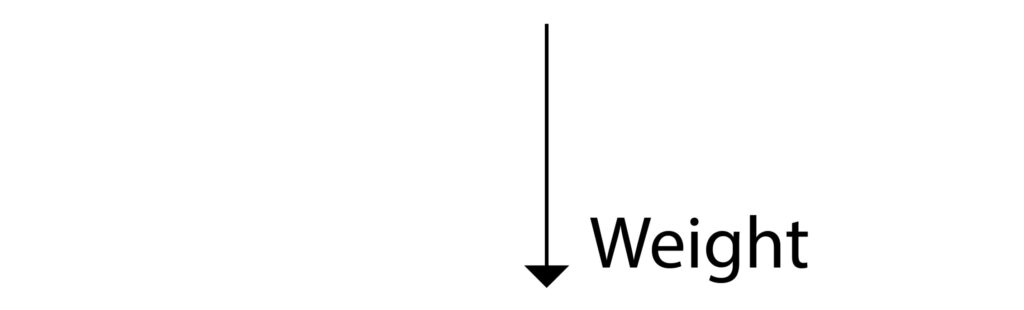
The weight acts directly downwards and each rope has its own tension force.We need to construct a free body diagram for this picture, see below:
We need to set a scale for the diagram 1cm = 10N. This means that the 40N weight force will have a 4cm downward arrow.
T2 has an angle of 45º from the horizontal and T1 has an angle of 20º from the horizontal
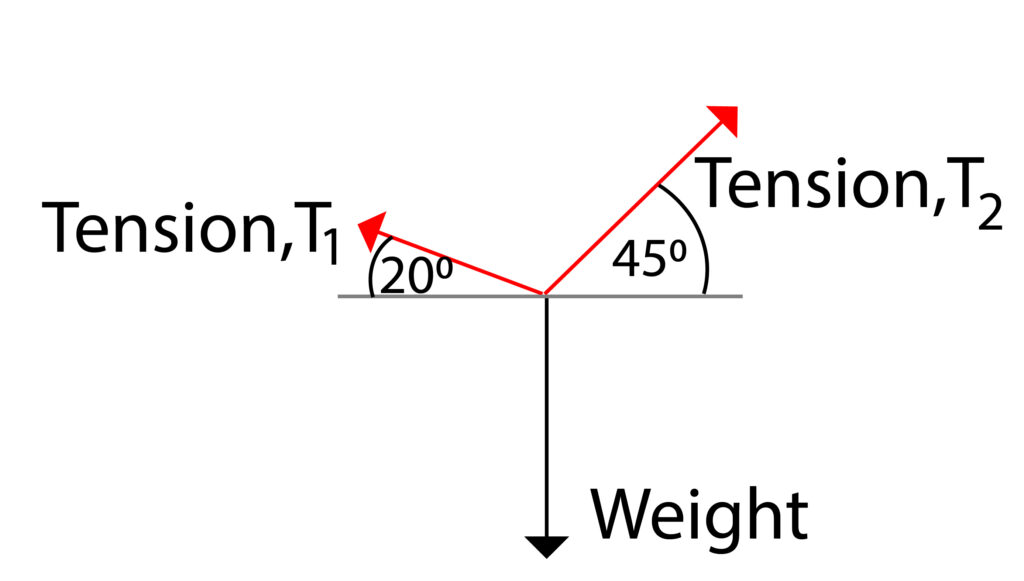
The diagonal force arrow for T2 should be longer than the diagonal force arrow for T1 because T2 is closer to the vertical.
Now we need to complete the parallelogram. First the weight force that is acting downwards would have an equivalent force arrow acting upwards from the centre that is equal in size, so draw this in as a 4cm arrow up from the centre.
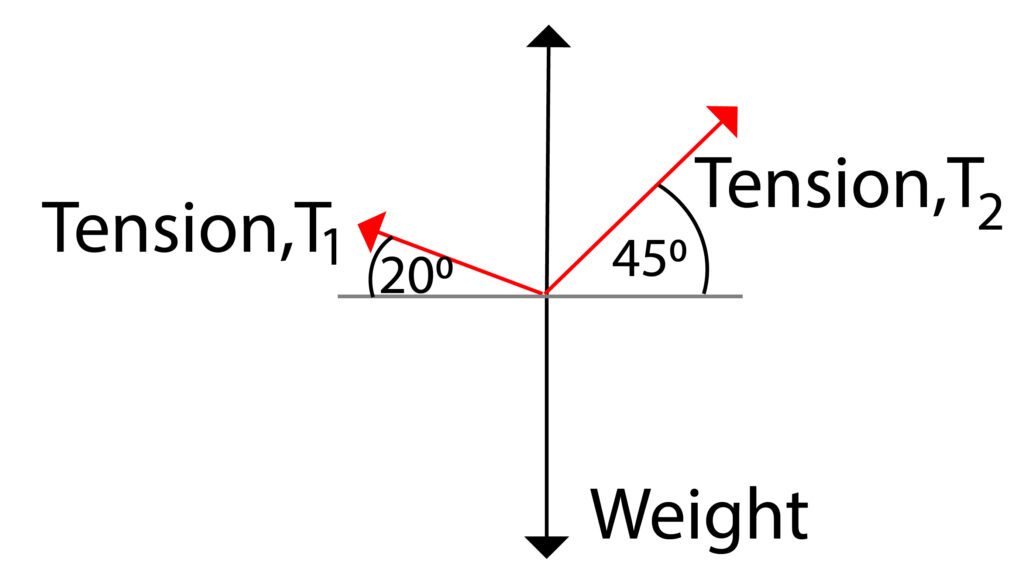
Now form the parallelogram, using two parallel lines.
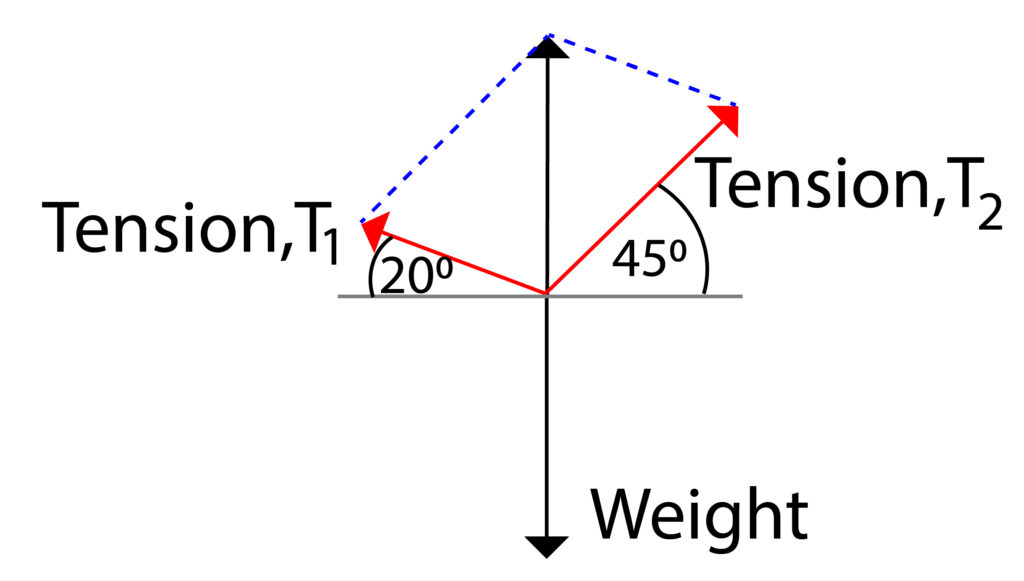
A perfect parallelogram has been produced. You may be asked to give the size of the forces T1 and T2.
Using the scale of 1cm = 10N. You can measure the length of T1 and T2, then apply the scale. In this case they should be approx 31N for T1 and 41N for T2
Practice Questions
1.A light bulb is suspended by two ropes to the ceiling as shown in the diagram below. The light bulb has a weight of 4N.
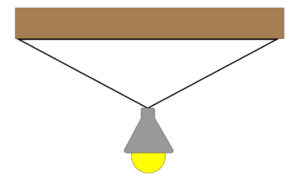
Draw a free body diagram for the forces acting on the object. Assume that the ropes form an angle of 30 degrees from the horizontal. You will need to use the parallelogram rule to help you to answer this question. A useful scale might be 1cm = 1N.
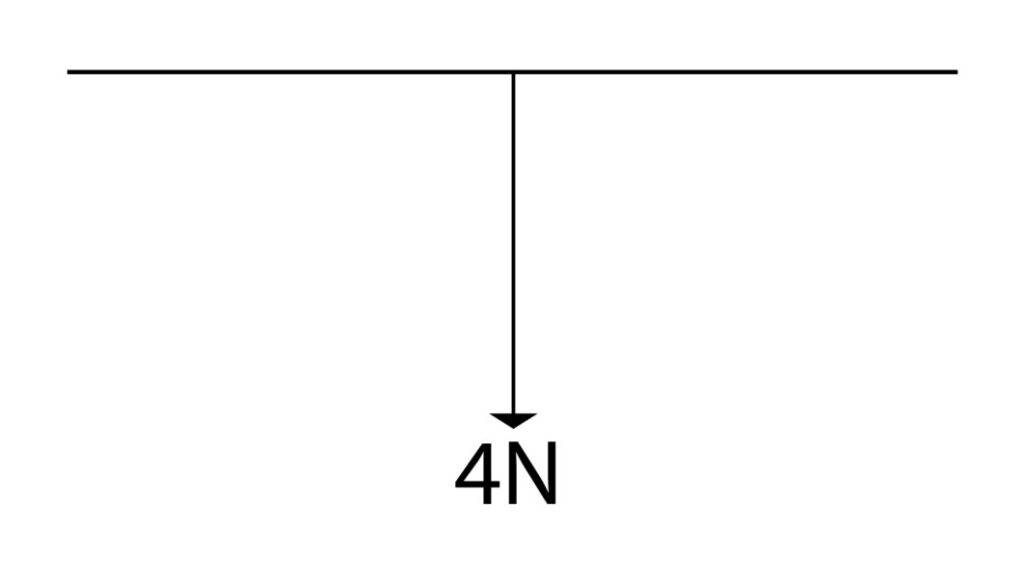
First draw a vertical arrow downwards. If we use a scale of 1cm = 1N, then we draw the downwards arrow 4cm long. Also place a horizontal line across the start of the arrow to represent the horizontal. This horizontal line allows you to put the angles in later.
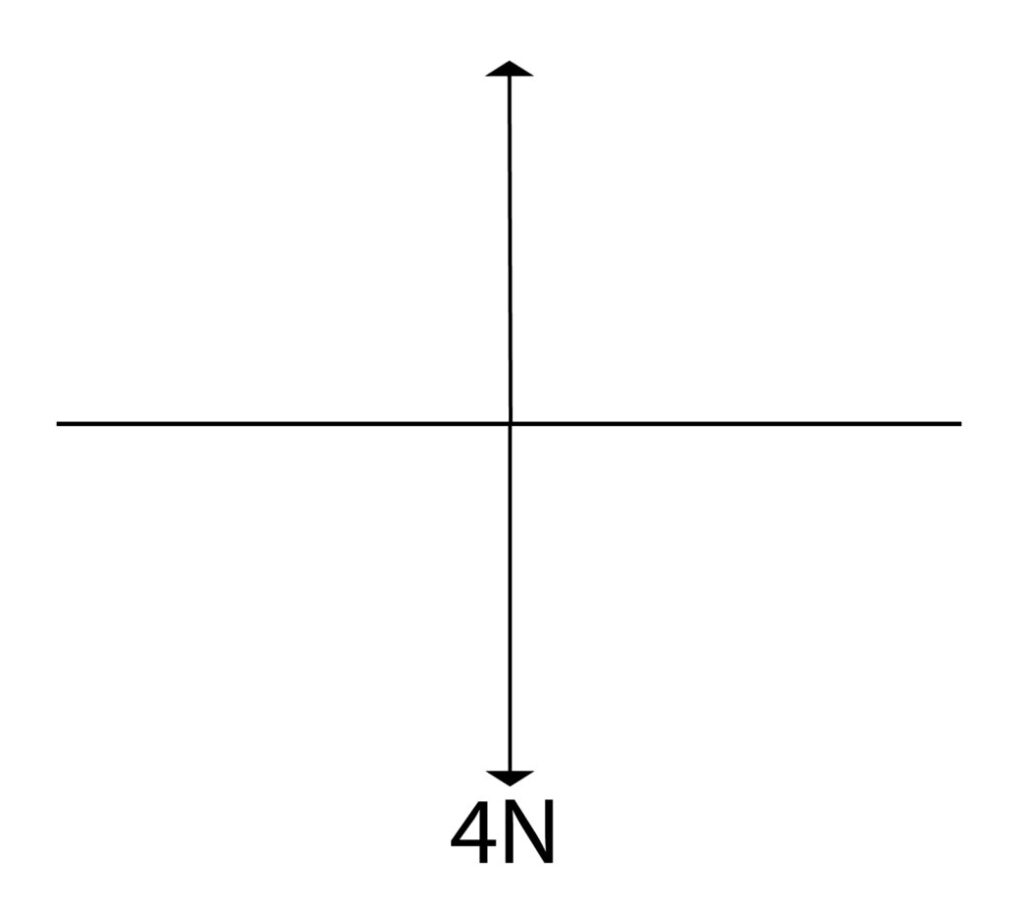
Now remember there will be an upward arrow which starts from the centre. This will be equal in size to the 4N downward arrow e.g. 4cm.
Now draw in the tension arrows using an angle of 30 degrees for the horizontal
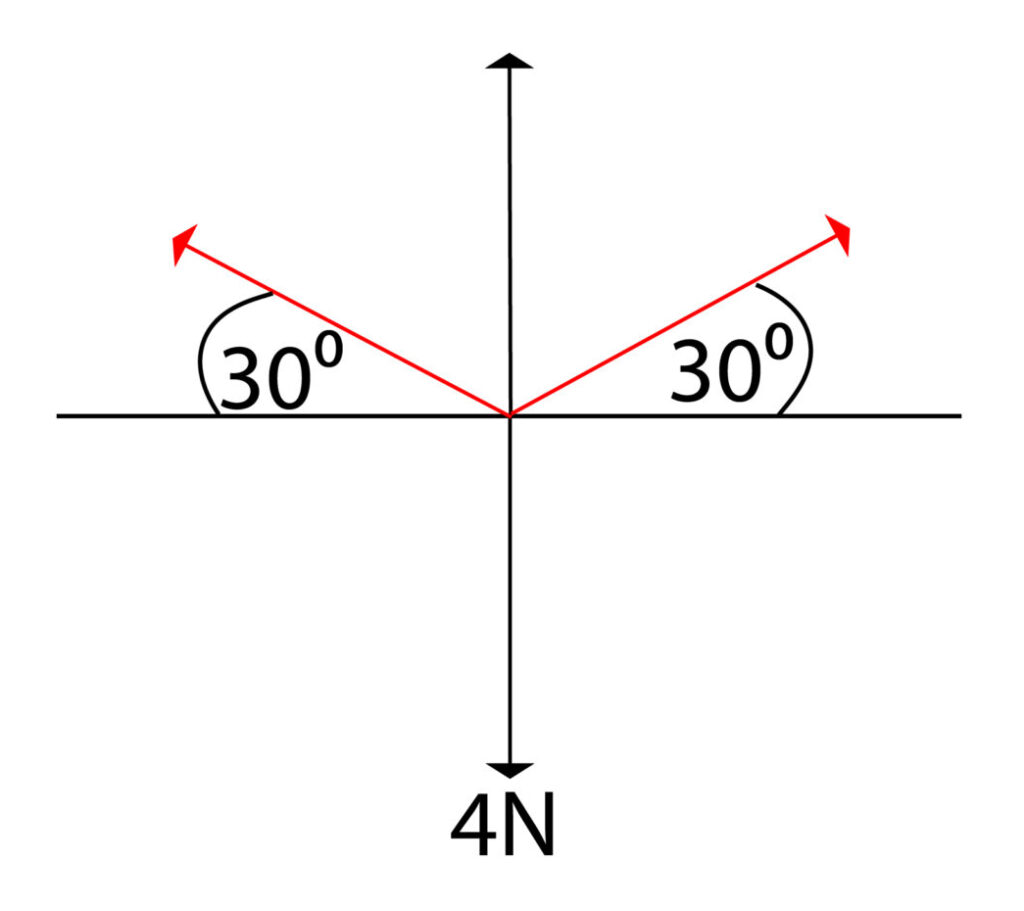
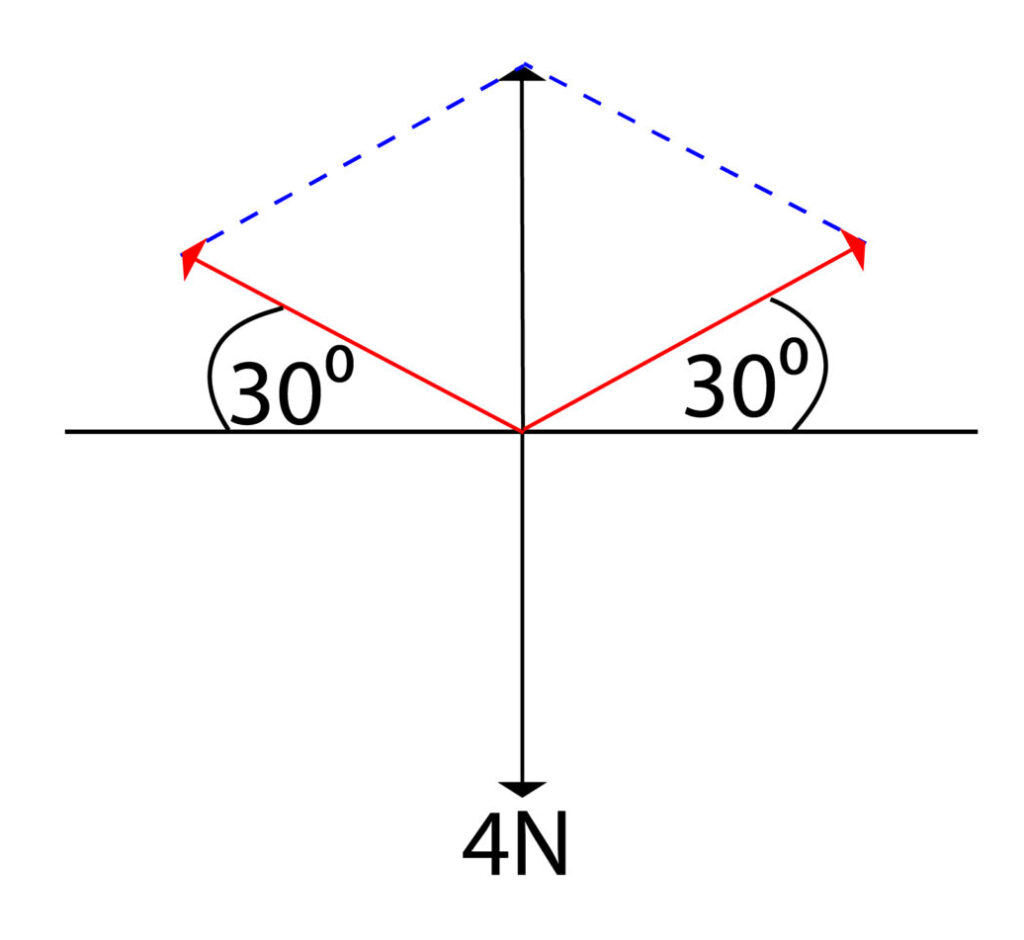
Now complete the parallelogram
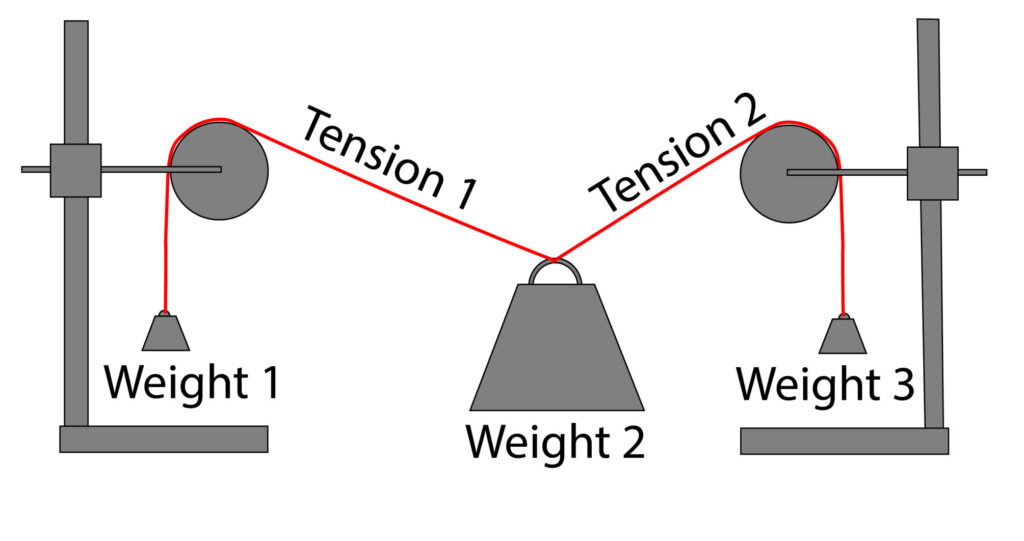
2. The diagram below shows a large weight in equilibrium.
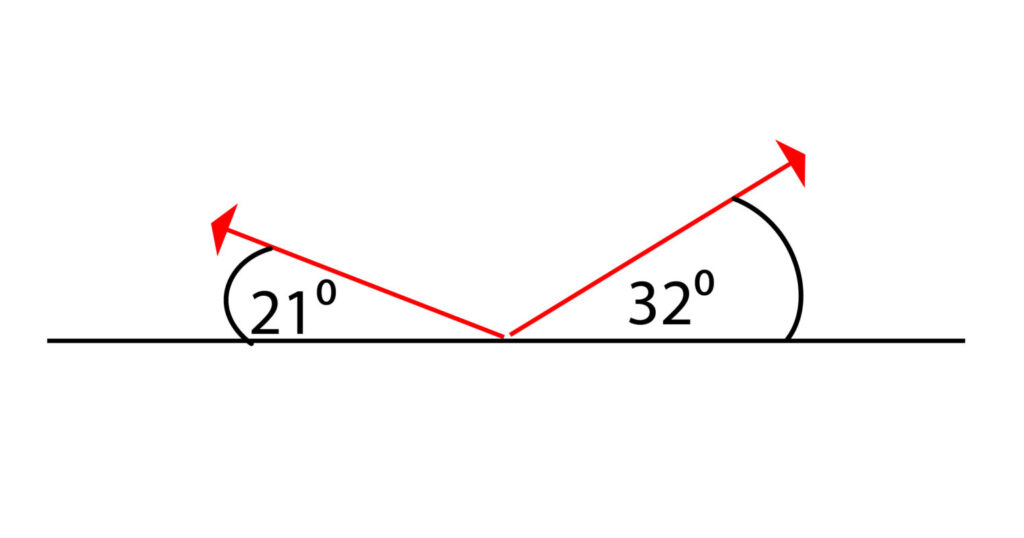
The line represented by Tension 1 is at an angle of 21º from the horizontal. The line represented by Tension 2 is at an angle of 32º from horizontal. You can assume that Tension 1 = 50N and Tension 2 = 56N.
Draw a free body diagram to show this, using a scale of 1cm = 10N. Then use this free body diagram and parallelogram rule to calculate Weight 2.
This time we need to start by drawing the horizontal line. Then draw on the tension forces Tension 1 which is 5cm (50N) and Tension 2 which is 5.6cm (56N), based on 1cm = 10N. Also, we need to include the angles of 21 degrees for Tension 1 and 32 degrees for Tension 2.
Lets now form the parallelogram
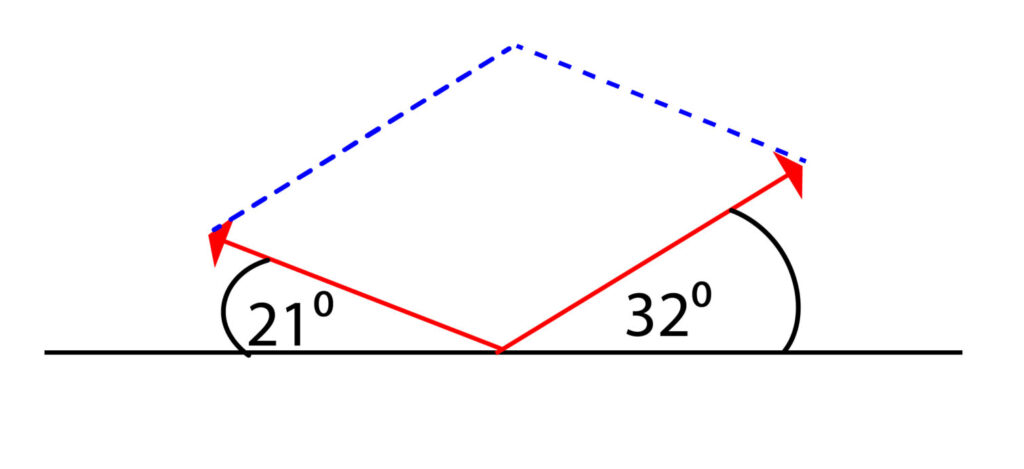
Draw a line to connect the top of the parallelogram to the bottom.
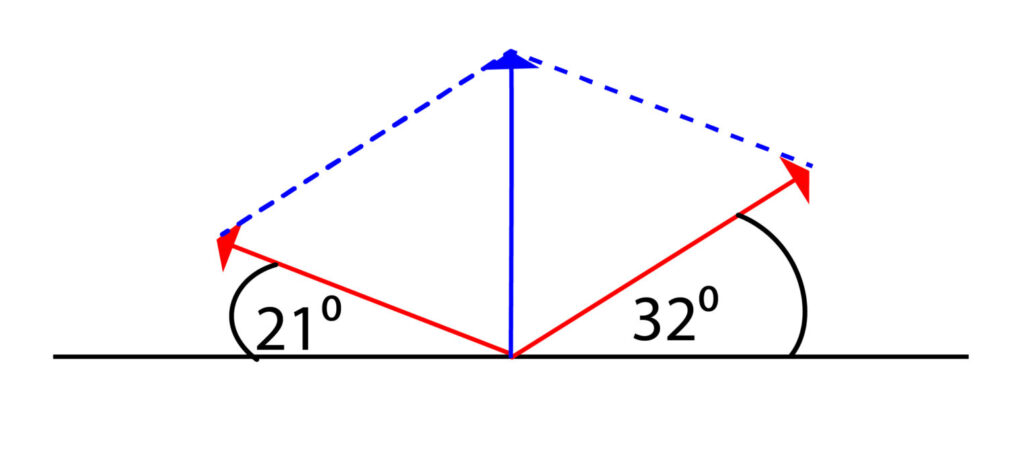
The weight force acting down will be the same size as the upwards force. Draw this arrow in pointing downwards, the same length as up arrow.
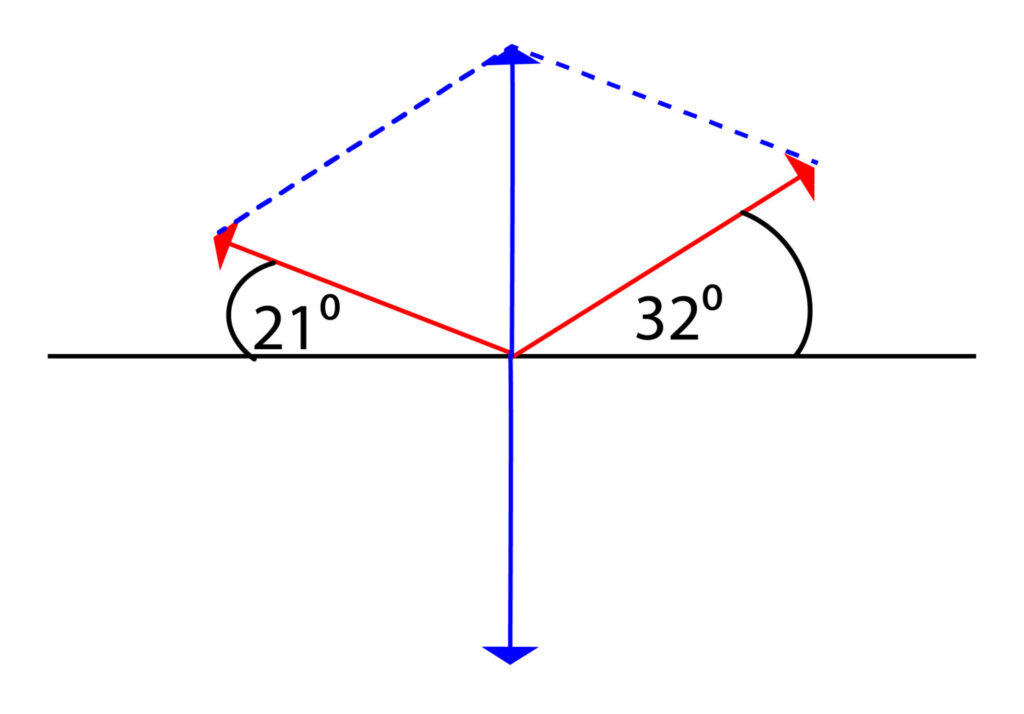
Now measure the weight arrow, downwards arrow from the centre, it is approx 6.5cm. 1cm = 10N, so this is a force of 65N approx.
Absorption and Emission of EM Radiation
JJ Thomson and Plum pudding model
Ernest Rutherford and the Nuclear Model
Niels Bohr changing the Nuclear Model
Discovering the Proton and Neutron
Measuring radiation from radioactivity
Radiation types and properties
Random nature of radioactive decay
Radioactive contamination or irradiation
Hazards of contamination and irradiation
Studies on the effects of radiation on humans
Different half lives of radioactive isotopes
Nuclear Fission Chain Reaction
Writing nuclear fission equations
Drawing ray diagrams for a concave lens
Drawing Ray Diagram to produce a virtual image for a convex lens
Drawing ray diagram to produce a real image for a convex lens.
Specular and Diffuse Reflection
Seeing Coloured Objects Part 2
Viewing objects through coloured filters
Transparent, Translucent and Opaque