AQA GCSE Pressure due to a column of liquid(Physics)
Pressure due to a column of liquid
Pressure in a liquid will increase with depth of the liquid. This is shown by the diagram below.

The deeper the hole is from the surface of the water, the further the water jet will travel. As the water jet travels further it must have a greater force, due to the water pressure being greater at increased depth below the surface.
If the holes in the water tank are all at the same depth from the surface of the water. Then each of the water jets travels the same distance because they all have equal force.

At the same depth, the same water pressure is present
Calculating the pressure of a liquid column.
Use the image below to answer the following question
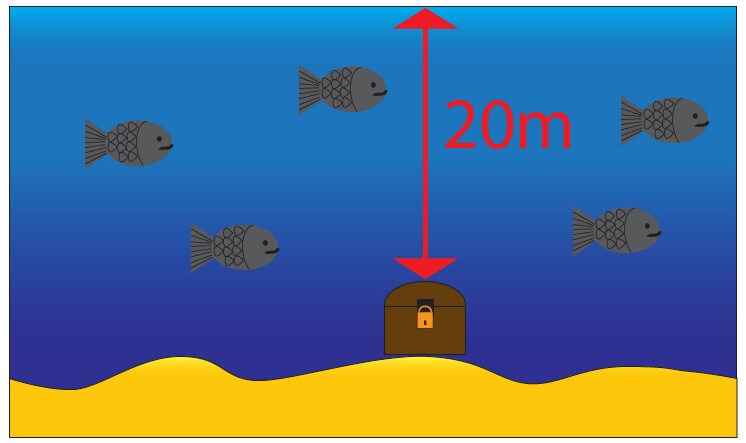
The treasure chest is located approx 20m below the surface of the water. Assuming that the density of sea water is 1020kg/m3 and gravitational field strength is 9.8N/kg calculate the pressure exerted on the treasure chest by the sea water.
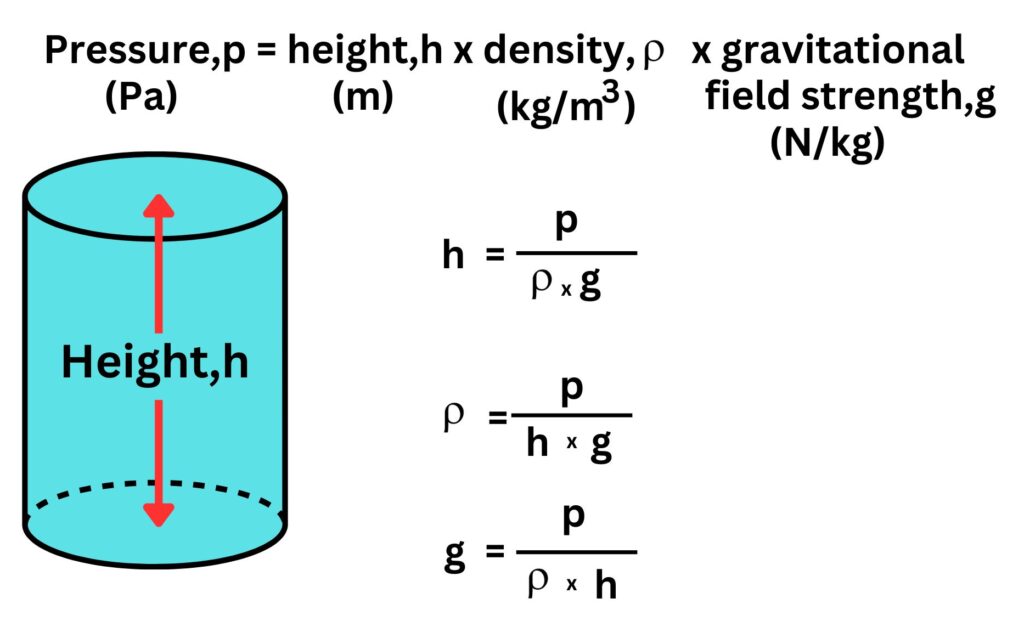
Pressure = height x density x gravitational field strength
Pressure = 20m x 1020kg/m3 x 9.8N/kg
Pressure = 199920Pa
Pressure = 200000Pa.
Practice Questions
1. A glass marble is dropped into oil as shown below:
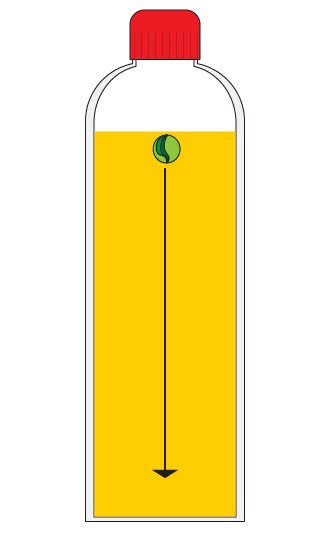
Describe how the pressure changes on the marble as it sinks lower in the oil.
2.A brick is at the bottom of a swimming pool 5m from the surface of the water. Density of water is approx 1000kg/m3.Calculate the pressure experienced by the brick.
(ignore any pressure effects due to atmosphere)
3. A submarine has been build to withstand a maximum water pressure of 6MPa. Assuming that sea water has a density of 1030Kg/m3. Calculate the maximum operating depth of the submarine in the water.
(ignore any presssure effects due to atmosphere).
Ignoring the effects of atmospheric pressure.
In the real world air is a fluid too, so ideally we should also take account of the atmospheric pressure and add that on as well. However, as a simplification in the questions above that has been ignored to simplify the question. Harder questions that target grades 8/9 may require you to add on the atmospheric pressure.
The diagram below shows a jar of water. There is a slight difference in density in the water from the top of the jar to the bottom. Water is more dense deeper because there is more weight of water from above.
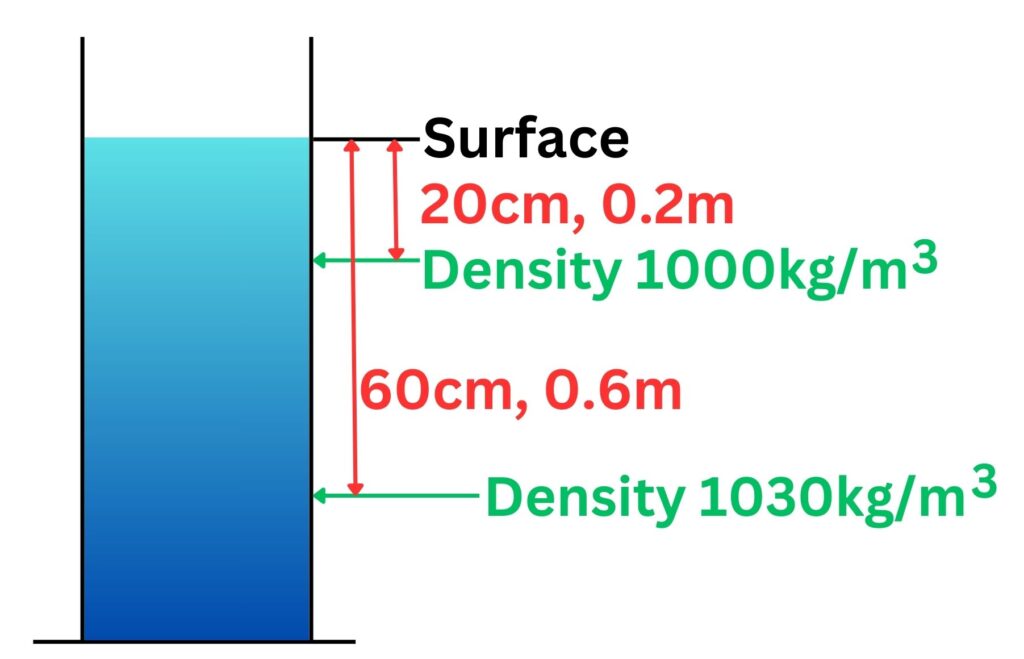 Calculate the difference in pressure between the two points labelled with the green arrows on the diagram above
Calculate the difference in pressure between the two points labelled with the green arrows on the diagram aboveIn order to do this we will work out the pressure at each of the two green arrows, using the following equation
Pressure = height x density x gravitational field strength
Pressure = 0.2m x 1000kg/m3 x 9.8N/kg = 1960Pa
Pressure = 0.4m x 1030kg/m3 x 9.8N/kg = 4038Pa
Difference in pressure = 4038Pa-1960Pa = 2078Pa
Absorption and Emission of EM Radiation
JJ Thomson and Plum pudding model
Ernest Rutherford and the Nuclear Model
Niels Bohr changing the Nuclear Model
Discovering the Proton and Neutron
Measuring radiation from radioactivity
Radiation types and properties
Random nature of radioactive decay
Radioactive contamination or irradiation
Hazards of contamination and irradiation
Studies on the effects of radiation on humans
Different half lives of radioactive isotopes
Nuclear Fission Chain Reaction
Writing nuclear fission equations
Drawing ray diagrams for a concave lens
Drawing Ray Diagram to produce a virtual image for a convex lens
Drawing ray diagram to produce a real image for a convex lens.
Specular and Diffuse Reflection
Seeing Coloured Objects Part 2
Viewing objects through coloured filters
Transparent, Translucent and Opaque