GCSE Work done and Elastic Potential energy

GCSE Work done and elastic potential energy

Work done and elastic potential energy

Work done means energy transferred. So, when work is being done, energy is transferred from one energy store to another.

Work can be done on springs to compress or stretch a spring.

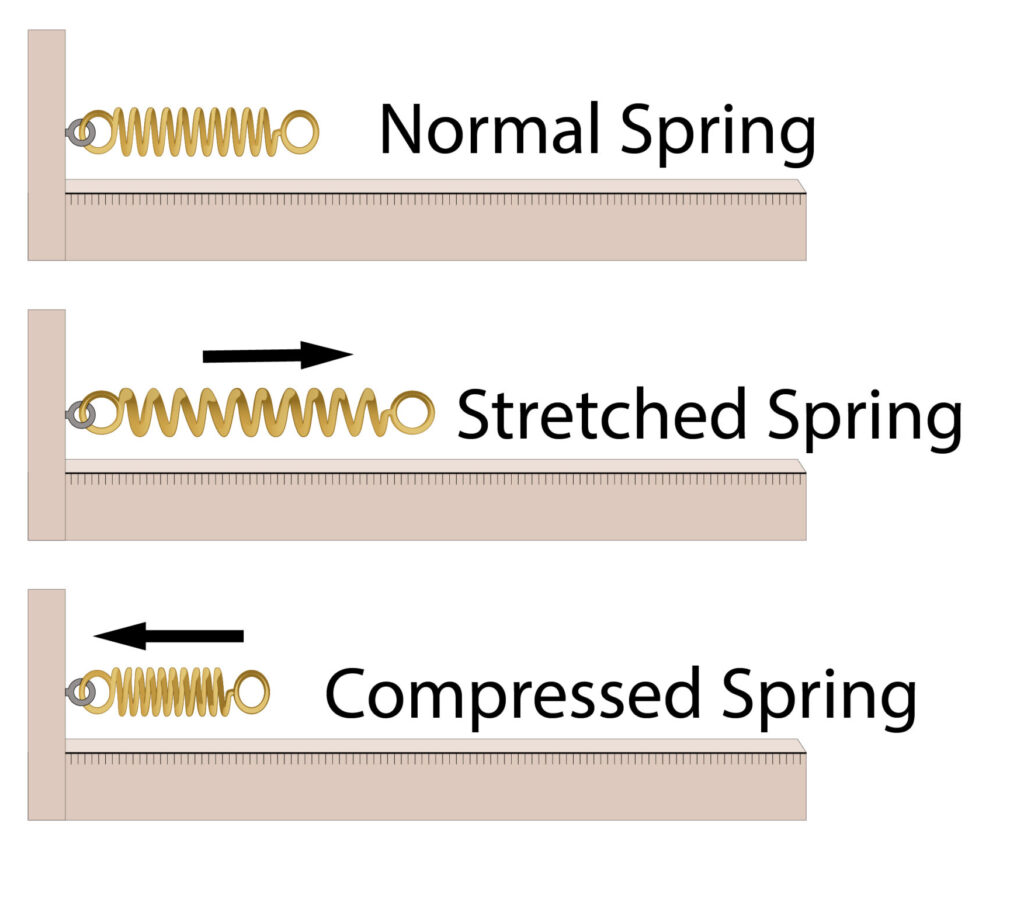
If a person applies a force by doing work to compress or stretch a spring, then the chemical potential energy store in their muscles will be mechanically converted into elastic potential energy of the spring.

Work done = Elastic potential energy?

During the linear (straight line) part of a force-extension graph, the work done will be equal to the elastic potential energy.

So, if 100J of work is done on the spring, then the spring will gain 100J of elastic potential energy.

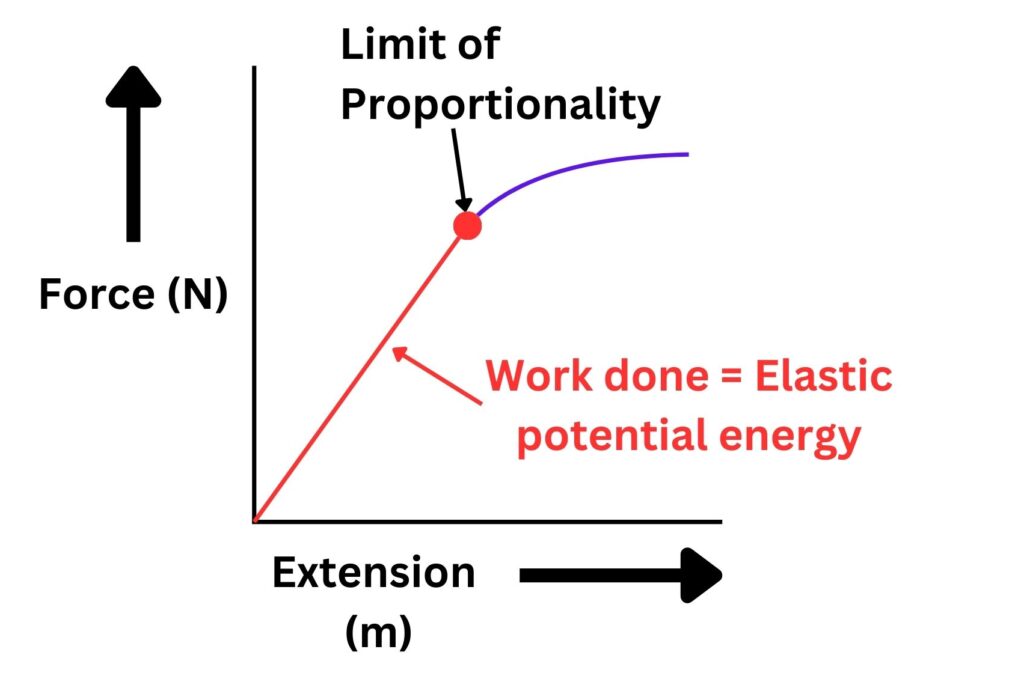
Beyond the limit of proportionality the work done will NOT be equal to the elastic potential energy. This part of the graph is represented by the curved purple line. The reason why, is beyond the scope of your course.

Elastic Potential Energy

Elastic potential energy is the energy stored in a material when it is compressed or stretched.

Sample Questions

In each of the following questions assume that the limit of proportionality has not been exceeded.

1.A spring has a spring contstant of 200N/m and its length is increased by 0.5m. Calculate the elastic potential energy stored in the spring.

E_e = 1/2 x k x e²

E_e = 1/2 x 200N/m x 0.5²

E_e = 25J

2. A spring has been compressed and its length decreased by 0.8m, the change in elastic potential energy was 30000J. Calculate the spring constant.

k = 2E_e/e²

k = 2 x 30000J/0.8²

k = 93750N/m

3. A stretched spring has 50000J of elastic potential energy and its spring constant is 100N/m. Calculate the extension of the spring

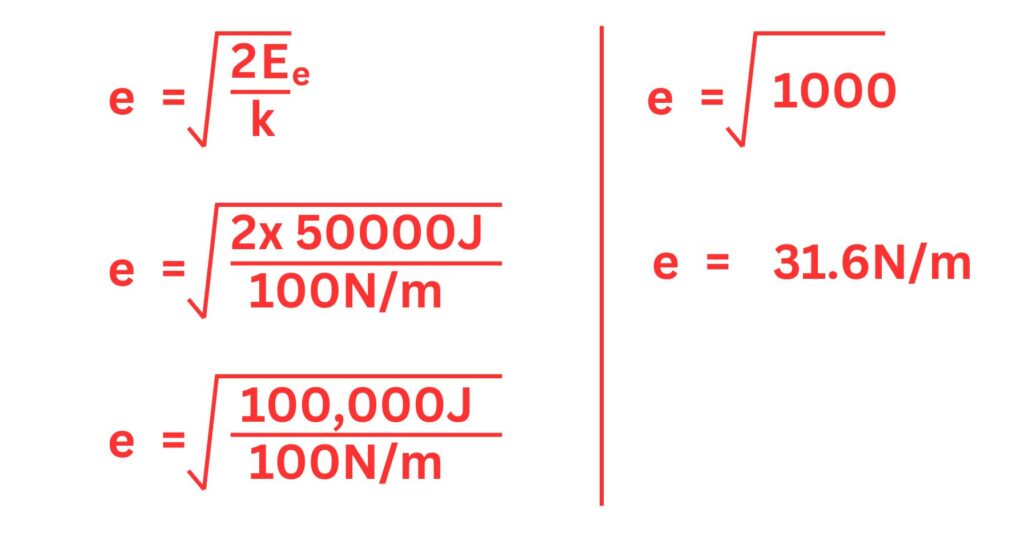
e = 31.6N/m

4. A spring has a spring constant of 300N/m and its length has increased from 20cm to 90cm. Calculate the elastic potential energy stored in the spring.

Convert the lengths into metres

20cm = 0.2m, 90cm = 0.9m

Extension = New length – original length

Extension = 0.9m-0.2m = 0.7m

E_e = 1/2 x k x e²

E_e = 1/2 x 300N/m x 0.72

E_e = 73.5J

5. The original length of a spring is 20m and its spring constant 80N/m. Whilst compressed the spring has an elastic potential energy store of 15000J. Calculate the compressed length of the spring.

First we need to calculate the extension

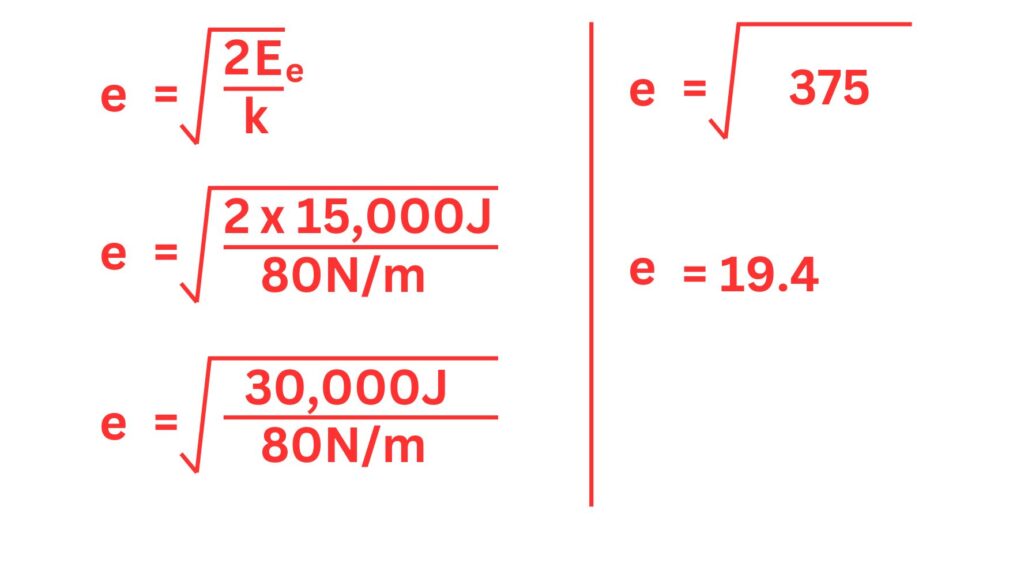
e = 19.4m

Therefore the compressed length of the spring is 20m-19.4m = 0.6m

Linking Work done and Elastic Potential energy

Whilst Hooke’s law applies and the force applied is directly proportional to the extension, then the work done is equal to elastic potential energy. This is shown by the graph above using the straight red line.

Below we have linked the two equations, work done and elastic potential energy. In addition we have rearranged the equations for you. It is likely that you may need this for the harder questions in the exam.